Allucinazioni Oggettive (II)

Ipotesi Materialiste su Formalismo e Intuizione in Matematica

Poiché abbiamo sostenuto, nella prima parte di questo articolo, che l’instabile equilibrio tra formalismo ed intuizione è uno dei motori della Matematica — ed è forse, al suo interno, quello fondamentale — cerchiamo ora di specificare la natura di entrambe queste capacità. Per farlo, proporremo due ipotesi materialistiche sulla natura mentale del formalismo e dell’intuizione Matematica.

Ipotesi sul Formalismo. Il formalismo è strettamente legato all’idea di una successione di tanti, piccoli passi elementari; passi singolarmente poco significativi, ma che uniti tra loro acquistano senso.

Il fatto che un simile tipo di comportamento possa dare dei risultati astratti, o che comunque riguardano solo l’informazione contenuta negli oggetti, ci viene quotidianamente confermato dal fatto che siamo riusciti a ideare e costruire macchine che funzionano proprio in questo modo. Gli smartphone sono, ad esempio, in grado tanto di trasmettere quanto di elaborare informazione.

Queste esperienze pratiche, ormai quotidiane, hanno anche una controparte teorica. Robin Gandy, un matematico inglese allievo di Turing, ha, infatti, dimostrato ¹ che ogni meccanismo che soddisfa le seguenti condizioni

• può essere montato (e smontato) a partire da pezzi indecomponibili con un numero finito di assemblaggi, ognuno dei quali coinvolge un numero finito di componenti,
• può funzionare solo attraverso successioni di catene cinematiche, ognuna delle quali è determinata da una aspecifica causa locale e che complessivamente non si ostacolano a vicenda,

può realizzare esattamente i comportamenti realizzati tanto dai computer o delle altre macchine che producono o trasformano informazione, quanto dai loro modelli astratti, come quello delle macchine di Turing.

Di conseguenza, non è difficile immaginare che il nostro cervello possa contenere delle strutture che si comportano come macchine di Gandy^{. 2}

Questo tipo di considerazioni, portate all’estremo, ha generato quella che viene chiamata Ipotesi Forte dell’Intelligenza Artificiale, per cui il cervello è un computer e la mente un programma.

Mondi chiusi (troppo) semplici. Il mondo strettamente formale ha certamente il vantaggio di essere un mondo semplice, dominato in tutti i suoi dettagli da una ‘bibbia’ di regole fisse e inviolabili.

Proprio per questo, un mondo strettamente formale è un mondo altrettanto strettamente chiuso e inalterabile. Agli occhi di un sistema linguistico, ad esempio, un’affermazione come:

questa frase è grammaticalmente scorretta

non può essere altro che falsa. Se infatti fosse vera, tale frase, non essendo stata generata dalle ‘sacre regole grammaticali’ che danno forma a quel mondo, semplicemente non esisterebbe.

una proprietà inerente all’intelligenza è che essa può saltare fuori dal compito che sta svolgendo per esaminare ciò che ha fatto. ³

Cosa molto difficile da realizzare quando un sistema non è intrinsecamente in grado di mettersi in discussione…

In effetti, tanto la storia della Matematica quanto l’esperienza dei suoi cultori, è intessuta di salti fuori dai sistemi, i quali, basandosi sull’analogia, hanno permesso di individuare sistemi più generali e che, basandosi sull’opposizione, hanno permesso di realizzare sistemi incompatibili con quelli esistenti, pur essendo altrettanto rigorosi…

E, parimenti, la storia individuale dei matematici è ricca di esempi di questi ‘lampi’ di pen­siero inaspettati, che ‘fanno vedere’ la soluzione di un problema. In effetti, l’esperienza quotidiana di ogni matematico militante si basa su intuizioni sorprendentemente vaghe e procede annaspando a sbalzi con ripensamenti troppo frequenti. Chiaramente, la logica così com’è non è in grado di dare una descrizione diretta né della crescita storica della Matematica né dell’esperienza quoti­diana dei suoi cultori. È anche chiaro che la ricerca di fondamenti definitivi mediante sistemi formalizzati non è riuscita a raggiungere nessuna conclusione convincente. ⁴

Ma c’è di ‘peggio’. Infatti, lo sviluppo della logica ha messo in risalto una proprietà limitativa altrettanto forte e significativa quanto l’impossibilità di superare la velocità della luce o dell’Indeterminazione di Heisenberg, ovvero il principio per cui

Nessun sistema può in nessun caso realizzare una operazione più complessa del sistema stesso.

E la precisione della Matematica ha permesso di verificare che essa è piena di concetti che hanno una complessità maggiore di quella realizzabile con le macchine di Gandy.

Per eliminare l’intuizione dal pensiero matematico, bisognerebbe quindi accoppiare alle attuali teorie formali una teoria altrettanto convincente su come dei ragionamenti formali, realizzati in maniera inconscia, si manifestino coscientemente come un salto conoscitivo, in cui la conclusione si presenta già pronta, senza passaggi intermedi.

Una teoria, cioè, che sia in grado di relegare tanto l’esperienza soggettiva dei matematici, quanto l’oggettiva complessità dei concetti che essi producono nell’ambito dell’illusione e dell’inesistenza.

Ipotesi sull’Intuizione. In alterativa si potrebbe, però, cercare di precisare — materialisticamente — le basi fisiche dell’intuizione, mostrando che i processi intuitivi possono essere concreti quanto quelli formali.

Così come il formalismo è strettamente legato all’idea di una successione di tanti piccoli passi elementari, l’idea di intuizione è legata a quella di un salto immediato, che presenta un prodotto mentale chiaramente definito in tutte le sue parti. Tanto che, nel tentativo di analizzare questa forma di pensiero, lo storico della Matematica Jaques Hadamard cita una lettera di Wofgang Amadeus Mozart, in cui egli narra che

[…] poi la mia anima si accende col fuoco dell’ispirazione. L’opera cresce; io continuo a espan­derla, concependola in modo sempre più chiaro finché ho l’intera composizione compiuta nella mia testa, per quanto lunga possa essere. Allora la mia mente la coglie nel suo insieme come uno sguardo del mio occhio comprende in sé un bel quadro o una bella giovane. Essa non mi viene come una successione di passi, con varie parti elaborate nei particolari, come verranno in seguito; ma la mia immaginazione me la fa udire nella sua interezza.

Vale la pena di cercare di ipotizzare qualche possibile meccanismo mentale che renda conto sia del ‘ronzio’ che precede questi salti sia della possibilità di raggiungere una conclusione evitando i passi intermedi.

Come spesso accade in questi anni, in cui le caratteristiche profonde della Meccanica Quantistica debbono ancora essere chiarite e rese compatibili con le caratteristiche meccanicistiche della Relatività Generale, ci si può rivolgere alla QM per cercare spiegazione ad ogni fenomeno strano, soprattutto se non deterministico. E, anche se il rischio di nascondere la polvere dei problemi irrisolti di altre discipline sotto il tappeto dei problemi irrisolti della QM è grande, tuttavia altrettanto grandi sono le sue potenzialità presenti.

Una di queste è la cosiddetta computazione quantistica, che oggi viene considerata soprattutto come un modo per ottenere gli stessi risultati dalle macchine di Gandy in maniera ‘infernalmente’ più veloce, ma che potrebbe anche dare la possibilità di progettare e costruire macchine quantistiche in grado di realizzare operazioni che nessuna macchina di Gandy sarebbe in grado di realizzare.

Proprio in questo senso, si è mosso Roger Penrose quando, nel tentativo di sviluppare una sua critica alla riduzione del pensiero ad un fenomeno meccanicistico, ipotizzò che la spiegazione dei comportamenti non meccanicistici della mente umana potrebbe trovarsi nelle pieghe più riposte della QM. ⁵ Penrose arrivò ad ipotizzare che particolari strutture presenti nei neuroni, i microtuboli, potessero essere la sede delle caratteristiche quantistiche del pensiero. Ed anche se le sue posizioni sono state e sono ancora ferocemente discusse, tanto dal punto di vista matematico quanto da quello fisiologico, esse rappresentano comunque un tentativo estremamente interessante.

Intuizione Quantistica? Seguendo questo esempio, ipotizziamo che i salti intuitivi possono essere collegati alla capacità di particolari sistemi quantistici di ‘rendersi conto’ di situazioni oggettive senza interagire con esse.

Una di queste situazioni è quella rappresentata dal meccanismo ⁶ schematizzato nel disegno che segue

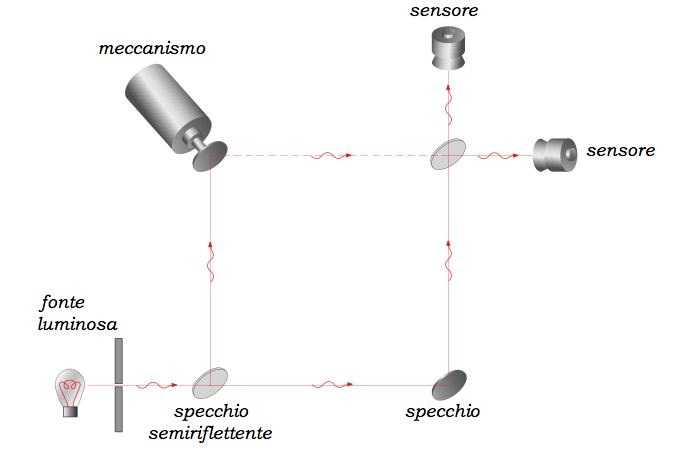
in cui la sorgente luminosa ‘spara’ un fotone per volta, gli specchi semiriflettenti possono riflettere o lasciare passare il fotone in maniera non deterministica, quindi imprevedibile a priori, e il meccanismo è in grado di bloccare o non bloccare il suo specchio, che, quando non è bloccato ed è colpito da un fotone, arretra interrompendo il percorso del fotone stesso.

In questo modo, un fotone sparato dalla fonte luminosa può andare prima verso destra e poi verso l’alto, oppure prima verso l’alto e poi verso destra, nel qual caso può essere bloccato dal meccanismo.

La descrizione quantistica di questo sistema non è in grado di stabilire dove passerà il fotone e riguarda esclusivamente le ‘probabilità’ ⁷ che il fotone abbia un certo comportamento. Essa è tuttavia in grado di stabilire che

• quando il meccanismo è settato in modo da lasciar passare il fotone, la probabilità che il fotone venga rilevato dal sensore in alto è nulla, mentre
• quando il meccanismo è settato in modo da non lasciar passare il fotone, esso può essere registrato, con la stessa probabilità del 50%, da entrambi i sensori.

In questo modo il sistema, sparando vari fotoni, è in grado di individuare quando il meccanismo interrompe o non interrompe uno dei possibili percorsi dei fotoni.

Quello che però è essenziale alle nostre considerazioni è che la descrizione precedente è valida, indipendentemente dal fatto che un fotone venga effettivamente bloccato dal meccanismo. Basta, infatti, che un fotone venga rilevato dal sensore in alto per essere sicuri che le probabilità che il meccanismo impedisca il passaggio del fotone sono del 100%. E quando il fotone passa dall’altra parte esso fornisce un’informazione certa sulla situazione del meccanismo senza interagire con esso!

Nella sua formulazione originale, il meccanismo era una bomba che poteva avere il detonare bloccato. Per verificare se lo stato del detonatore nell’ambito della fisica classica, si sarebbe potuto solo provare ad attivarlo, facendo così esplodere le bombe non difettose. Ma utilizzando il precedente apparato, nel suo complesso, siamo in grado di distinguere le bombe con il detonatore bloccato da quelle funzionanti senza necessariamente farle esplodere. C’è, infatti, una probabilità del 25% che il nostro interferometro stabilisca che la bomba è funzionante senza interagire con il suo detonatore.

Per questo, commentando il loro risultato, Ashalom Elitzur e Lev Vaitman sostengono di aver mostrato che è possibile ottenere alcune informazioni su una regione di spazio senza alcuna interazione con tale regione, né nel passato né nel presente. ⁸

D’altra parte, proprio queste considerazioni quantistiche (forse congiunta alla presenza di bombe), mi hanno riportato alla mente quella che mi sembra un vivacissima descrizione delle nostre capacità intuitive e della loro importanza. Si tratta di un passo di Remarque che, pur non riguardando una forma ‘culturale’ di intuizione, fa capire la sua basilare funzione biologica:

Di colpo, al primo tuonare di una granata, torniamo con una parte di noi stessi indietro di migliaia di anni. È un intuito puramente animale quello che in noi si ridesta, che ci guida e ci protegge.

Incosciente, ma assai più rapido, più sicuro, più infallibile che non la coscienza. Non si può spiegare; si va senza pensare a nulla ed ecco che ad un tratto ci si trova in un avvallamento del terreno, mentre sopra noi volano schegge di granata, ma non ci si ricorda di aver sentito venire il colpo né di aver pensato a coricarci. Se ci si fosse lasciati guidare dal ragionamento, si sarebbe a quell’ora un carname sparpagliato: è stato l’altro che oscuramente vigile in noi ci ha buttati a terra e salvati, senza che noi si sappia come. Se questo altro non fosse, da un pezzo, fra le Fiandre e i Vosgi, non vi sarebbero più creature viventi. ⁹

Computer Intuitivi?. Allontanandoci dalle bombe, ipotetiche o reali, proviamo a vedere se questa possibilità di ‘sapere senza interagire’, può esser usata per dare una base materiale alla — oggettivamente meno rischiosa, ma soggettivamente altrettanto impressionante — intuizione Matematica.

Dato che l’aspetto essenziale dell’interferometro di Elitzur­­­–Vaidman non riguarda la natura del meccanismo, ma il fatto che lo specchio montato su di esso sia o non sia in grado di muoversi, possiamo sostituire la bomba con una porta logica che, ricevendo input digitali, costituiti da 0 e 1, segnala — poniamo — l’output 0 bloccando lo specchio e l’output 1 lasciandolo libero.

Se ci trovassimo in una situazione classica, l’unico modo per sapere quale sia l’output di tale porta logica sarebbe quello di andare a verificare se lo specchio è mobile o è fisso. In ambito quantistico, invece, sparando vari fotoni nel nostro interferometro, dovremo solo verificare se un fotone interagisce con il sensore in alto per sapere che le probabilità che l’output della porta sia 1 sono del 100%. E questo senza avere nessuna interazione con la porta in questione…

E siccome i circuiti che fanno funzionare i nostri attuali computer non sono altro che complessi aggregati di porte logiche, sostituendo ciascuna di queste porte con uno dei precedenti interferometri potremmo ottenere un ‘computer intuitivo’ in cui è possibile ‘eseguire’ un calcolo senza dover interagire con nessuno dei passaggi che lo realizzano…

Naturalmente, per fare in modo che una simile possibilità abbia una probabilità significativa di realizzarsi bisogna lavorare ancora molto. Tuttavia, la cosa è, in linea di principio, fattibile. L’esistenza di questo tipo di apparati quantistici permette, quindi, di considerare l’ipotesi per cui la possibilità di ottenere un risultato senza interagire con il sistema che lo realizza, sia un modo di spiegare l’esperienza dell’intuizione (Matematica).

Se nel nostro cervello ci fossero delle strutture in grado di realizzare le precedenti operazioni, il sottostante ‘ronzio’ che accompagna le giornate di chi si occupa di un significativo problema matematico potrebbe essere associato al ‘lancio dei fotoni’ nel corrispondente sistema, mente il ‘lampo’ intuitivo che, quando va bene, dà una svolta a questi tentativi avrebbe la stessa chiarezza complessiva e la stessa mancanza di dettagli costruttivi di una certezza probabilistica…

E quindi… Mozart — lo disturbiamo nuovamente — sosteneva che

la musica non è nelle note, ma tra le note.

Analogamente, la Matematica non è nelle formule, ma tra le formule. E forse anche dietro di esse.

Gli aspetti formali della Matematica potrebbero, infatti, non essere altro che la punta di un iceberg, visibile proprio perché spinta in alto da un’immensa quantità di ragionamenti sommersi, legati per lo meno all’intuizione…

Un bel problema matematico, che riporta all’oggettività delle sue allucinazioni. Ma anche — penso — un problema psicologicamente interessante… che proprio la relativa semplicità e ‘nettezza’ del pensiero matematico — dove si ha a che fare con triangoli piuttosto che con sentimenti o pulsioni — potrebbe rendere metodologicamente significativo…

Antonio Vincenzi ©

Vai alla prima parte

Note:

1 – Church’s Thesis and Principles for Mechanisms. In: The Kleene Symposium. Nort–Holland 1980. 

2 – Un interessante tentativo, in questo senso, è illustrato in Vallortigana G., Panciera N.: Cervelli che contano. Adelphi 2014. 

3 – Hofstadter D.R.: Gödel, Escher, Bach: una eterna ghirlanda infinita. Trad. it.: Einaudi 1984. 

4 – Feferman S.: What Does Logic Have Tell Us About Mathematical Proof? Mathematical Intelligencer 2, 1971. 

5 – Ombre sulla mente. [Trad. It.] Rizzoli 1996. 

6 – che tecnicamente si chiama interferometro di Elitzur–Vaidman, dal nome dei fisici che lo hanno descritto nell’articolo Quantum Mechanical Interaction–Free Measurement, Fundation of Physics 23, 1993. 

7 – Tecnicamente sono qualcosa di diverso, che tuttavia afferisce alle stesse caratteristiche concettuali della probabilità. 

8 – Is it possible to know about something without ever interacting with it? Vistas in Astronomy 37, pp. 253­–256, 1993. 

9 – Niente di nuovo sul fronte occidentale. Cap. IV.