Sommario
Questo articolo, trattando i problemi di relazioni esistenti tra arti diverse, si collega alla presentazione di Daniela Gariglio e Pier Paolo Strona “Dipinti e Musica in risonanza psicoanalitica e matematico-geometrica” al Convivium tenutosi in Fiuggi, in cui musiche di vari autori, eseguite al pianoforte da Pier Paolo Strona, sono state associate, in base a considerazioni sulle rispettive strutture geometriche e sulle atmosfere ed emozioni suscitate, a dipinti di Daniela Gariglio, psicoanalista/scrittrice, che ne ha evidenziato alcune risonanze psicoanalitiche che vanno nel senso dei suoi studi su trauma e adattamento creativo.
Introduzione
In tutte le arti l’artista crea le sue opere utilizzando uno specifico linguaggio, intendendo il linguaggio come un insieme di regole di grammatica e di sintassi, regole di composizione per scrivere poesie, testi, musica, per dipingere, scolpire, progettare opere architettoniche, regole espressione di culture diverse e in continua evoluzione nei secoli e nei luoghi.
Il termine “linguaggio” ci fa subito pensare alla letteratura e alla poesia, ma ogni arte ha un linguaggio proprio, dalla musica alle arti figurative, alla scultura, all’architettura, alla fotografia, al cinema e così via.
Riflettendo sulle caratteristiche di questi linguaggi, si scopre abbastanza facilmente che tutti, anche se specifici e apparentemente diversi tra di loro, hanno in realtà molti elementi in comune, e tra questi gli elementi geometrici sono particolarmente importanti e determinanti nella concezione e nella realizzazione delle singole opere.
Mettere a fuoco e comprendere questi elementi non solo consente un maggior approfondimento di conoscenza delle opere stesse, ma permette di collegarle, metterle in relazione tra di loro, allargando lo sguardo a comprendere le varie forme d’arte come un qualcosa di più unitario, tutte frutto di ambienti culturali che si sono evoluti nella storia e nella geografia, tutte opera dell’uomo.
Nell’articolo si vuole dare un piccolo contributo di riflessione su questo vastissimo tema prendendo in considerazione alcuni semplici elementi geometrici e cercando di vedere come li si ritrovi nelle varie arti e come siano determinanti nel processo creativo degli artisti.
Dopo alcune considerazioni sull’idea del “bello” legato ai rapporti, alle proporzioni, all’essenzialità e alla completezza nell’arte, ci si soffermerà su un elemento geometrico semplicissimo, il segmento, e si parlerà delle trasformazioni geometriche, concludendo con alcune considerazioni sull’idea di infinito.
I rapporti e le proporzioni
Le proporzioni, i rapporti tra le parti sono elementi geometrici e sono sempre stati considerati nella cultura occidentale elementi base per definire il “bello” [1, 2]. Sono concetti espressi e sviluppati da Pitagora, Platone, Agostino e poi da Alberti, nel secolo XV, esuccessivamente da Diderot e da Cartesio.
Nelle arti plastiche e figurative le proporzioni tra le parti sono sempre state fondamentali nella creazione artistica.
La proporzione aurea, forse la più importante, ha attraversato l’arte di tutti i secoli, soprattutto a partire dal Medio Evo, quando è stata associata al “Divino”, dimenticata un po’ nell’epoca barocca e poi tornata ad affermarsi nel XX Secolo, arrivando a determinare in modo assoluto ed esasperato ad esempio l’opera di Mondrian.
In musica, molti secoli prima, l’uomo aveva imparato a scegliere alcuni suoni tra gli infiniti esistenti in natura definendo i rapporti tra le loro frequenze, con criteri matematici e geometrici, e organizzandoli in sequenze, in scale [3]. Non solo quindi le proporzioni come misura del bello di un’opera ma anche come criterio con cui preparare il materiale per poi realizzarla.
Pitagora, all’origine della musica occidentale, aveva così creato la scala “pitagorica”, come sequenza di rapporti tra lunghezze di una corda o tra pesi diversi e questi rapporti erano espressi da numeri piccoli, 2/1 (ottava), 3/2 (quinta), 4/3 (quarta), e così via. Molti secoli dopo, con J.S. Bach, si è poi definitivamente affermata la “scala temperata” a 12 suoni, ma altre scale con diverse scelte di semitoni, quarti di tono, microtoni [3] hanno aperto la strada a mondi creativi diversi. Scale con un numero di toni diverso infine sono state usate in altre parti del mondo in molte culture musicali, ad esempio la scala pentatonica.
Dal XV secolo in poi, sotto l’influsso dell’Alberti e sullo sfondo di una aspirazione ad unificare tutte le arti molto sentita a quei tempi, questi rapporti tra i suoni, espressi da numeri piccoli, erano stati utilizzati come proporzioni fondamentali dai pittori nella creazione delle loro opere.
Più avanti, negli anni tra la fine del XIX secolo e l’inizio del XX, con l’avvento della società industriale, si è avuta una vera rivoluzione nel linguaggio di tutte le arti, della musica e della letteratura, con una sempre maggior interazione tra loro e con evoluzioni parallele dei linguaggi. Alcune figure hanno contribuito in modo particolare a questa evoluzione, Il musicista Scriabin [1] parlava di colori in musica, inventando il “pianoforte a colori”, e il pittore Kandinski parlava di suoni in pittura [4] nei suoi scritti, confrontandosi in un lungo carteggio con Schoenberg.
Le teorie di composizione, musicali e grafiche, sviluppate in quegli anni sono poi passate alla nuova arte nata a metà del XIX secolo, la fotografia: il fotografo cerca gli stessi equilibri, le stesse forme del pittore, dello scultore, dell’architetto, ma non le può progettare, deve trovarle guardandosi intorno[2]. Si accorge allora che queste proporzioni sono create dalla luce,
Anche i pittori, tempo prima, a partire da Caravaggio, se ne erano già accorti e avevano cominciato ad usare non solo le linee del disegno per comporre le opere, ma anche le linee create dalla luce e gli spazi colorati.
Nel XX secolo poi le sequenze di fotografie, il cinema quindi, aveva introdotto nell’arte figurativa la quarta dimensione, quella del tempo, dimensione essenziale nella musica, ma fino ad allora presente nelle opere figurative solo come percorso di osservazione di un’opera in effetti statica. SuI problema del tempo lavoreranno in particolare i futuristi italiani tentando di introdurre nelle loro opere la sensazione del movimento vero e proprio.
La terza dimensione, invece è sempre stata un grande problema sia per i musicisti, profondità del suono ricercato con il cromatismo ad esempio, sia per i pittori, legati ad uno spazio bidimensionale.
Si vede dunque da queste brevi osservazione su arti e musica come la soluzione di problemi geometrici sia sempre stata una molla potentissima nella creazione artistica, capace di aprire agli artisti orizzonti vasti.
Essenzialità e completezza
Oltre a quello delle proporzioni e dei rapporti tra le parti costituenti un’opera d’arte, esiste anche un altro aspetto della “bellezza” che accosta i linguaggi delle arti e della musica a quelli della matematica e della geometria, aspetto che si potrebbe sintetizzare nel motto “il più con il meno”, ma aggiungendo anche che nel “meno” ci deve essere tutto quello che è necessario. L’opera d’arte che risponde a questi concetti riuscirà ad esprimere e comunicare il suo messaggio di bellezza e di conoscenza con la massima efficacia.
Nel linguaggio simbolico della matematica un’equazione può dire molto di più di un volume di decine di pagine, un’espressione matriciale può condensare in una riga migliaia di equazioni e consente di operare su di esse, presentandosi al contempo in forme che rispondono a concetti estetici di eleganza e di bellezza.
In musica si potrebbero analizzare sotto questo punto di vista le opere dei grandi, pensiamo all’essenzialità e alla ricchezza delle composizioni di Bach e di Mozart ad esempio, dove nulla è fuori posto, nulla è superfluo e nulla manca.
J.S. Bach [5] opera come un grande architetto che concepisce strutture complesse ed essenziali: l’architetto usa elementi semplici e li combina creando opere relativamente gigantesche che possono essere belle o brutte, ridondanti o essenziali, eleganti o sgraziate a seconda delle sue capacità; Bach lavora nello stesso modo, usando elementi, cellule semplici, ma combinandole insieme in modo fantastico a costruire opere, gigantesche, strutture perfette complete ed essenziali, e per questo bellissime.
Mozart con pochissime note traccia linee perfette in cui nulla manca e nulla è di troppo, usando spesso anche il silenzio, l’assenza di suono, per creare drammaticità e attesa.
Naturalmente il fatto di ottenere “il più con il meno” non significa che il “meno” sia piccolo. Pensiamo alla quantità di note presenti nelle opere della seconda metà del XIX secolo, forse non sempre e non tutte essenziali: forse sarebbe interessante analizzare e confrontare su questo aspetto le opere dei maggiori compositori di quel tempo, Brahms, Ciaikowski, Rachmaninoff, ad esempio.
Analogamente in fotografia l’essenzialità e la completezza dell’immagine è spesso determinante per la sua capacità di comunicare bellezza e conoscenza.
Il fotografo cerca di cogliere momenti e situazioni create dalla luce per realizzare immagini che possano raccontare storie o esprimere concetti complessi che a volte nulla hanno a che fare con il soggetto reale fotografato, esprimendo graficamente concetti che richiederebbe molte pagine per essere espressi. La nostra mente è capace di trasfigurare la realtà osservata e la può interpretare simbolicamente per esprimere e raccontare altro [6].
Un esempio di espressione di concetti in un’immagine si può vedere in figura 1, dove si è fotografata una parte di un grattacielo in cui ogni finestra riflette uno stesso dettaglio del grattacielo di fronte ma la deforma in modo diverso.
Questa immagine si può interpretare come una sintesi del pensiero che Luigi Pirandello ha espresso nelle sue opere, “Così è se vi pare”, “Uno, nessuno, e centomila” e altre: ognuno filtra la realtà a modo suo, forse la “verità” sta dove le finestre riflettono il sole, dove c’è la luce, ma lì non si riesce a distinguere più nulla e quindi non abbiamo accesso alla verità assoluta, ognuno ha la sua.
Esempi di fotografie che raccontano una storia invece si possono vedere nei due esempi delle figure 2 e 3.
“Agonismo” (Fig.2) rappresenta la storia di una partita in cui a contendersi il pallone sono due giocatori della stessa squadra, mentre “Disperazione” (Fig.3) credo non abbia bisogno di commenti e si racconti da sola.
Il segmento
Geometricamente un segmento è una parte di retta di lunghezza definita, un elemento semplicissimo eppure fondamentale nel linguaggio della musica e delle arti.
Nella musica, il ritmo, una tra le principali componenti del discorso musicale, insieme alla melodia, all’armonia e al timbro, si può rappresentare graficamente come una sequenza di “segmenti temporali di lunghezza variabile”. Ma il ritmo non è solo un elemento del linguaggio musicale, lo si ritrova ovunque nell’arte e anche nella letteratura; l’azione in un film, in una rappresentazione teatrale o in una danza ha un suo ritmo che la caratterizza, una poesia infine ha una sua metrica.
Proprio la coerenza ritmica sta alla base della creazione di opere in cui più arti sono presenti, una canzone ad esempio, testo e musica, la colonna sonora di un film.
Una canzone, un lied, musica e testo poetico, ha solitamente un ritmo unico, elemento fondamentale per legare tra loro suoni e parole. Analogamente nel cinema, la musica che descrive una scena ne rispetta anzitutto il ritmo, oltre a creare un’atmosfera coerente con le situazioni raccontate. Formidabile ad esempio sotto questo punto di vista la “battaglia sul ghiaccio” di S. Prokofiev che accompagna il racconto di S. Eisenstein nel film “Alexander Nevskij”.
Viceversa è possibile creare animazioni che commentino e visualizzino musiche preesistenti, come nel film Fantasia di W. Disney. Interessante in particolare l’episodio “l’apprendista stregone” che ricrea con l’animazione la musica di P. Dukas, che a sua volta si era ispirato all’omonima Ballata di W. Goethe: cinema, musica, letteratura strettamente collegate da una base ritmica, da una sequenza di segmenti temporali.
In tutti i casi precedenti il ritmo regolava la posizione degli elementi delle opere nel tempo.
Considerando invece le arti plastiche e figurative, il ritmo è quello che regola la posizione delle parti nello spazio, come in architettura e in pittura. In fotografia il fotografo [7,8] lo cerca e lo trova guardandosi intorno, osservando soprattutto quello che la luce crea in quel momento, come nelle figure 4a/b, dove il riflesso del sole sulle ringhiere di balconi (Fig.4a) crea una geometria astratta (Fig.4b), una linea spezzata fatta di segmenti, che non ha più nulla a vedere con il soggetto fotografato.

Fig. 4a: Alba con riflessi (foto P.P. Strona)
In Architettura infine il ritmo non regola soltanto l’organizzazione dello spazio tridimensionale e la disposizione degli elementi strutturali, ma può essere fondamentale anche nelle sue superfici piane come, ad esempio, in un fregio: illuminante a questo proposito la rappresentazione con notazione musicale fatta da Bouleau [1] del ritmo con cui si succedono le figure nei fregi del Partenone.
Le trasformazioni geometriche
Traslazioni, rotazioni, inversioni, retrogradazioni, isometrie, aumentazioni e diminuzioni, omotetie, e così via sono tutte trasformazioni usuali in geometria e matematica.
Sono però anche tutte operazioni che i compositori hanno sempre fatto e continuano a fare nello scrivere le loro composizioni, applicandole a sequenze di note di varia lunghezza e complessità, giocando così a costruire e sviluppare un discorso e a variarlo [5].
Si possono osservare direttamente nella scrittura sul pentagramma ma diventano evidenti se invece delle note si utilizza una rappresentazione di funzioni in un sistema cartesiano.
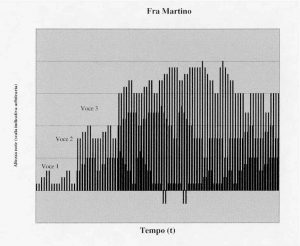
In musica qualunque melodia infatti può essere rappresentata in un sistema di riferimento cartesiano come una funzione y=f(x)[3] in cui x è la variabile tempo e y l’altezza del suono. Il ritmo corrisponde alle durate nel tempo dei diversi suoni, lunghezza quindi di segmenti sull’asse x. Una composizione polifonica sarà descritta da più funzioni nello stesso grafico.
Come esempio in figura 5 si rappresenta l’incipit del celebre canone “Fra’ Martino” con tre voci che entrano in successione, sfasati nel tempo e ad altezze diverse [5].
La struttura di una composizione musicale, e anche il modo con cui un compositore l’ha creata, può essere compresa meglio se la si rappresenta graficamente.
In generale nella costruzione di una sua opera il compositore ha a disposizione innumerevoli possibilità di sviluppo e di elaborazione che corrispondono a trasformazioni geometriche: se trasla ad esempio una melodia, o una semplice sequenza di note, ad altezze diverse nello spazio sonoro, realizza così una “progressione”, se la presenta rovesciata rispetto a un piano orizzontale (inversione) o retrogradata rispetto a un piano verticale, letta cioè dall’ultima nota alla prima (specchio) apre orizzonti vasti alla sua fantasia creativa.
L’uso di queste operazioni in musica, vere e proprie trasformazioni geometriche, e la loro rappresentazione grafica cartesiana è stato ampiamente trattato da matematici e musicisti [5,9].
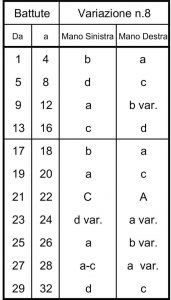
In [10], a titolo di esempio, viene in tal modo analizzata la Variazione Goldberg n. 8 di J.S. Bach (Fig. 6): osservandola in forma grafica si scopre facilmente che qui Bach ha utilizzato due idee musicali molto semplici, una per la mano sinistra e una per la mano destra e le ha esposte nella prima battuta, ne ha fatto il retrogrado (specchio) ottenendo altri 2 elementi (Fig.7a), e ha poi composto l’intera variazione traslando nello spazio dei suoni questi 4 elementi e combinandoli in tutti i modi possibili (Fig.7b), creando così un bellissimo, essenziale e fantasioso puzzle, un gioco geometrico realizzabile a tavolino.

Fig. 6: J.S. Bach, Variazione Goldberg n. 8
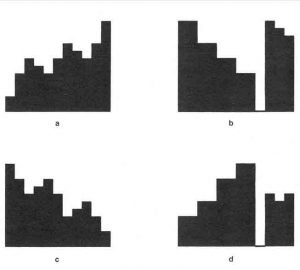
Fig. 7: Elementi base in forma grafica
La rappresentazione grafica della musica inoltre può suggerire anche altri sviluppi intuibili, se si pensa ad esempio alla possibilità di percorrere il cammino inverso: creare cioè materiale musicale a partire da un quadro o da una fotografia. Sempre in [10] si è fatta un’operazione di questo tipo, proponendo un insieme di regole che lo consenta e applicandolo a titolo dimostrativo a un caso particolare, la composizione di un piccolo corale a partire dalla fotografia di una catena montuosa.
Le trasformazioni geometriche sono dunque strumenti potentissimi nella creazione di opere musicali, ma non solo. In tutte le arti in realtà l’artista opera in modo analogo con gli elementi con cui crea la sua opera, organizzandoli su una superficie piana il pittore, il fotografo, il regista di un film, in uno spazio tridimensionale lo scultore, l’architetto, il regista di uno spettacolo teatrale, di un balletto. Anche lo scrittore e il poeta in ultima analisi organizzano con criteri geometrici gli elementi delle loro opere.
L’infinito
L’idea di infinito sta nella mente umana, spazio infinito, orizzonte, tempo infinito, eternità, e anche nell’arte e nella musica gli artisti hanno cercato di renderne in qualche modo l’idea.
Esempi in musica sono il canone perpetuo, una forma musicale che non ha mai fine, o la mazurka op. 68 n. 4 di F. Chopin, scritta nelle ultime settimane di vita, con una struttura armonica che non giunge mai a conclusione, musica che va avanti all’infinito.
In geometria un esempio interessate di forma collegata in qualche modo all’idea di infinito è il nastro di Möbius, matematico e astronomo tedesco del XIX secolo.
Tutte le superfici hanno una faccia esterna e una interna e per passare dall’una all’altra occorre attraversare un bordo; il nastro di Möbius invece ha un solo lato e, se ci si muove su di esso, si passa senza accorgersene, senza discontinuità di bordo quindi, alla faccia opposta per poi ritornare a quella di partenza. Continuando a muoversi sul nastro si ha dunque la sensazione di muoversi all’infinito. Si costruisce prendendo un foglio rettangolare e unendo i lati minori dopo aver ruotato uno dei due bordi di 180 gradi.
J.S. Bach, circa 100 anni prima, senza ovviamente conoscerlo, aveva utilizzato questa figura nel Canone n.1 della sua “Offerta musicale”: i dettagli della costruzione di questo canone sono ben illustrati in [11].
Il nastro di Möbius, forse perché collegato in qualche modo all’idea di “infinito” ha interessato anche altri artisti, tra gli altri M.C. Escher (1898-1972) che ha realizzato alcuni disegni (Nastro di Möbius I, Nastro di Möbius II) basati sul nastro. Più recentemente anche lo scultore svizzero Max Bill (1908-1994), ha creato una scultura, “Endless ribbon”, sulla cui superfice ci si può muovere all’infinito, realizzando nel marmo un nastro di Moebius.
Conclusioni
Grandi e stretti sono i legami tra le varie arti e per lo più nascono da elementi presenti nei vari rispettivi linguaggi, elementi principalmente di tipo matematico e geometrico. Su questa base si può pensare quindi di proporre esperimenti che colleghino arti diverse, ad esempio musica e fotografia.
Le attività di musicista e fotografo, sviluppate con continuità in tutta la vita, mi hanno facilitato in tal senso spingendomi a tentare esperimenti di questo tipo; l’incontro con pittori mi ha aperto la strada per collegare analogamente musica e dipinti: è quanto ho cercato di fare negli ultimi anni in alcune Università, scuole e associazioni culturali[4], associando l’ascolto di composizioni musicali alla visione di opere pittoriche e fotografiche capaci non solo di suscitare emozioni congrue, ma anche con strutture geometriche apparentabili. Per quanto riguarda l’emozione, lascio però il campo allo psicoanalista che si occupa proprio di affetto, anche quando parla di relazione e creatività.
© Pier Paolo Strona
Abstract
Nell’articolo si prendono in considerazione alcune caratteristiche dei linguaggi che gli artisti utilizzano nella creazione delle proprie opere, indagandone soprattutto gli elementi che hanno in comune e creando in tal modo una base di riferimento per mettere in relazione tra loro arti diverse. Si può così approfondire meglio la conoscenza e la comprensione delle singole opere, collocandole in un orizzonte più ampio e vasto. Il discorso è focalizzato in particolare sulla musica e sulle arti plastiche e figurative, includendo in queste ultime anche quella storicamente più recente, la fotografia.
Riferimenti Bibliografici
[A] C. Bouleau, “La geometria segreta dei pittori”, Editions du Seuil, 1963 (edizione italiana Electa, 1988)
[B] P. Boulez, J.P. Changeux, P. Manoury, “I neuroni magici, musica e cervello”, Carocci Editore, 2016
[C] H. Partch, “Genesis of a Music”, Da Capo Press, 1974
[D] V. Kandinskij, Punto, linea, superficie, Adelphi Edizioni, 1968
[F] G. Donati, P.P. Strona, “Nel Giardino delle Meraviglie, Una passeggiata all’ombra delle Variazioni Goldberg di J.S. Bach”, Trauben, Torino, 2008 http://www.arty.it/pierpaolo-strona/musica/musica_studi.php
[G] P. Baranowski, Perception and Interpretation (based on the work of Decentrism’s artists) International Journal of Design & Nature and Ecodynamics, WITPress, Vol.7 n.4, 2012
Download: http://www.witpress.com/elibrary/dne-volumes/7/4/637
[H] P.P. Strona, “Capturing the light”, LIGHT 2011, International Conference on Light in Engineering, Architecture and the Environment, May 2011, Poznan, Poland
Download: http://www.witpress.com/elibrary/wit-transactions-on-the-built-environment/121/22069
[I] P.P. Strona, “Discovering reality through the camera”, International Journal of Design & Nature and Ecodynamics, WITPress, Vol.7 n.4, 2012
Download: http://www.witpress.com/elibrary/dne-volumes/7/4/638
[L] B. Scimeni, “Contrappunto musicale e trasformazioni geometriche” Atti del Convegno “Matematica e Cultura”, Venezia, 1997, Springer Verlag
[M] G. Donati, P.P. Strona, “Nature and Music: a general method for designing a composition from an image”, International Journal of Design and Nature, WITPress, UK, Vol. 6, n. 1, 2011
Download: http://www.witpress.com/elibrary/dne-volumes/6/1/501
[N] https://www.youtube.com/watch?v=iN9fGDnWcFY
[1] Era affetto da sinestesia, capacità di fondere insieme sensazioni provenienti da sensi diversi, ad esempio la vista e l’udito.
[2] Gli sviluppi recenti della fotografia digitale e dei SW di post-processamento stanno però aprendo nuove opportunità ai fotografi ed agli artisti che intendono utilizzare la fotocamera per creare delle opere originali e di forte impatto visivo ed emozionale, pur partendo sempre e comunque da immagini fatte di luce. Si veda a questo proposito il sito “Private Landscapes” di Luigi Piero Ippolito:
http://luigipieroippolito.wixsite.com/lpi-century.
[3] Anche se la musica viene percepita come un flusso sonoro continuo, tuttavia essa è costruita come un insieme di singole note: si tratta quindi di un sistema discreto e la f(x) è in effetti un istogramma.
[4] Università di Rennes, Architettura (2015), Università di Palma di Mallorca (2016), Fondazione Croce (Torino, 2013), Liceo artistico “Cottini” (Torino, 2016), Fotogruppo “L’incontro” (Collegno, 2016), Circolo degli Artisti, (previsto a Torino, 2017)
Pier Paolo Strona ha sentito fin dai primi anni stimoli e interessi verso tre campi apparentemente lontani e diversi tra loro, la musica, la fotografia e l’ingegneria, ed è riuscito a coltivarli e a dedicarvisi a livello professionale con continuità, integrandoli in una visione unitaria. Gli studi musicali iniziati a 5 anni lo hanno portato, allievo del Maestro Maffiotti, al diploma in pianoforte all’Accademia Filarmonica di Bologna nel 1962, anno in cui si è iscritto al Politecnico di Torino, laureandosi in ingegneria civile e specializzandosi in strutture metalliche nel 1968. La fotografia invece, a partire dal 1956, lo ha sempre accompagnato nelle sue attività, alpinismo, vela, viaggi, amore per la natura, e anche ingegneria, con servizi fotografici nei cantieri. L’interesse per la scienza si è concretizzato in attività di ricerca nel campo dei metodi numerici per l’analisi strutturale, in particolare il Metodo degli Elementi Finiti (FEM). La fotografia è stata intesa essenzialmente come “arte figurativa”, realizzazione di immagini nate guardandosi intorno, affinando la propria sensibiltà a vedere cose che spesso sfuggono ai più, comunicazione di conoscenza, bellezza ed emozioni. Anche la musica è stata coltivata con lo stesso spirito di ricerca, esplorando la letteratura europea e occidentale classica e contemporanea, allargando l’interesse alle musiche americane, asiatiche e africane. Più recentemente si é accostato all’organo e allo studio della letteratura organistica, particolarmente della musica italiana dal XVI al XVIII secolo. Negli ultimi anni ha esposto le proprie fotografie in mostre personali e ha suonato in Italia e all’estero per Associazioni culturali, Enti pubblici, Istituti universitari e ha prodotto alcuni CD.
Maggiori informazioni si possono trovare nel suo sito web http://pierpaolo-strona.arty.it